Das Abstraktionsproblem besteht darin, dass man Systemzustände und keine Systemkomponenten betrachtet.
In Markovdiagrammen verbirgt sich hinter jedem Zustandssymbol immer das gesamte System, allerdings in einem spezifischen Zustand.
Das rechte Beispiel mit dem zweistrahligen Flugzeug verdeutlicht dies auf anschauliche Weise.
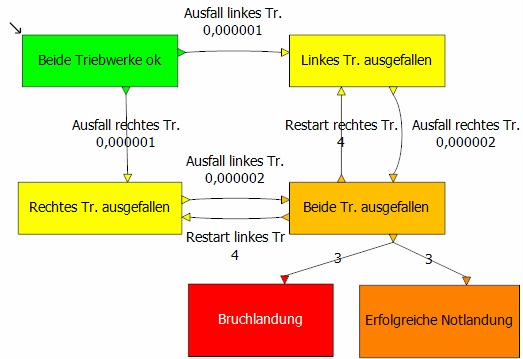
Dieses Beispiel zeigt recht anschaulich die Vorteile der Markovmethode, und es lohnt sich durchaus, dieses Beispiel etwas ausführlicher zu erklären:
