
Belastbarer
Umgang mit technischen
Unsicherheiten
Statistik,
RAMS
& Qualitätsmanagement
Zuverlässigkeits-Blockdiagramme
Zuverlässigkeits-Blockdiagramme dienen zur Visualisierung und
analytischen Behandlung komplexer Systeme. Das System wird in einzelne
Funktionsblöcke zerlegt, deren Zusammenwirken das Systemverhalten
wiederspiegeln. Interessant und eigentlich erst notwendig wird dieses
Verfahren dann, wenn das System nicht lediglich aus einer seriellen
Kette aus Funktionsblöcken besteht, sondern komplizierter aufgebaut ist
und beispielsweise folgende Eigenschaften aufweist:
- Parallelstrukturen
(Redundanzen),
- Fehlertolerantes Verhalten
- Maschenstrukturen
(Produktionslinien)
- spezifische
Wartungsphilosophien, die zur analytischen Behandlung ein Auftrennen
des Systems in Teilsysteme notwendig machen.
Die Funktionsblöcke, sowie ein
Startpunkt und ein Endpunkt, werden entsprechend der Systemarchitektur
mit Pfeilen verbunden. Solange es mindestens einen funktionsfähigen
Pfad vom Startpunkt über die Funktionsblöcke zum Endpunkt gibt, wird
das System als funktionsfähig angesehen.
Ein zweistrahliges Flugzeug möge als Beispiel dienen; dieses Beispiel
wird auch im Kapitel Markovanalyse
verwendet, und zeigt sehr deutlich
die Unterschiede zwischen Zuverlässigkeits-Blockdiagrammen
und Markovdiagrammen auf.
Zweistrahlige Flugzeuge müssen so ausgelegt sein, dass sie bei Ausfall
eines Triebwerkes sicher bis zum nächstgelegenen Flughafen
weiterfliegen können. (Freilich stellt diese Situation eine Luftnotlage
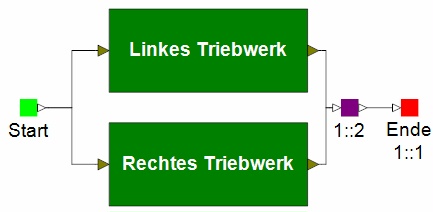
dar). Das Blockdiagramm ist dementsprechend aufgebaut: Vom Startpunkt
erfolgt der Funktionsfluss im Normalfall über beide Blöcke (Triebwerke)
bis zum Endpunkt. Die Zusammenführung vor dem Endpunkt besagt mit dem
Symbol 1::2, dass einer der beiden Teilpfade ausreicht, um das
Gesamtsystem am Laufen zu halten.
Mit Zuverlässigkeits-Blockdiagrammen kann man -je nach Mächtigkeit der
verwendeten Software- verschiedene Parameter berechnen, beispielsweise:
- Ausfallrate, MTBF
- Zuverlässigkeit
- Verfügbarkeit
- Reparaturkosten und -dauern
- Optimale Wartungsintervalle
- Optimale Ersatzteilbevorratung
Die Eigenart dieses Beispiels, auch
im
Hinblick auf das Kapitel Markovanalyse, besteht darin, dass das
Blockdiagramm bei Ausfall beider Blöcke zwar ein Systemversagen
wiederspiegelt, dies allerdings nicht unbedingt die Betriebspraxis
wiedergibt: Das Flugzeug kann nämlich auch ohne Triebwerke für immerhin
~ 10 Minuten sicher gleiten. Während dieser Zeit wird es der Besatzung
wahrscheinlich gelingen, wenigstens eines der beiden Triebwerke wieder
zu starten und damit doch noch bis zum nächsten Flughafen zu
kommen.
Weiterhin lässt diese Diagrammdarstellung unberücksichtigt, dass bei
Ausfall eines Triebwerkes das jeweils andere mehr leisten muss und
seine Ausfallwahrscheinlichkeit dann etwas höher ist.
Blockdiagramme können derartige Systemeigenschaften nicht wiedergeben,
Markovdiagramme dagegen schon.
Datenschutzhinweise
MTBF Berechnung
beauftragen Was bedeutet MTBF

